
Modeling makes math both important and interesting!
What is Math Modeling?
Mathematical modeling refers to the process of creating a mathematical representation of a real-world scenario to make a prediction or provide insight. Real-world issues can be complex and messy. While it can sometimes feel intimidating to get started, the open-ended nature of real-world problems leads to building and applying problem solving skills, creativity, innovation, and mathematics.
What does the math modeling process look like?
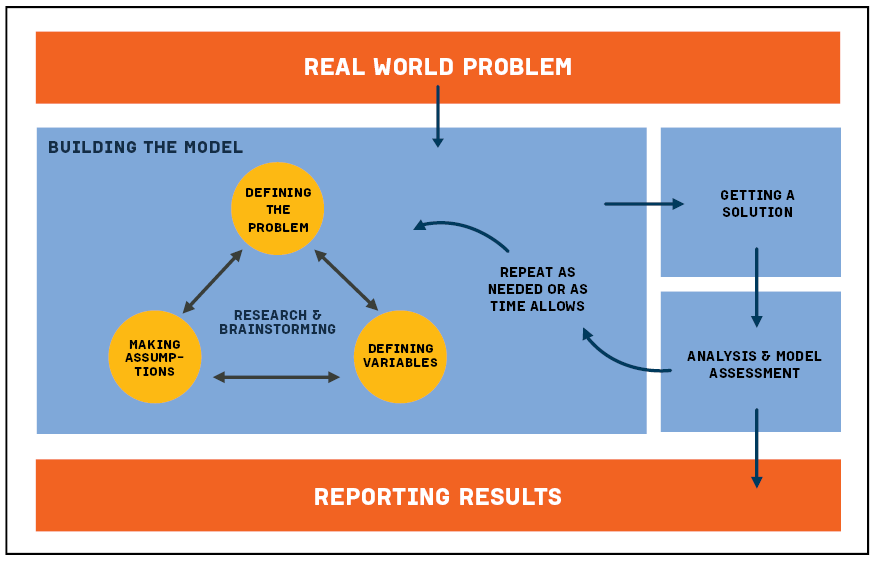
Mathematical modeling can be thought of as an iterative process made up of the following components:

Make Assumptions
It is impossible to account for all the factors in a given situation, so the modeler must make choices about what is important to include.

Define the Problem
Modeling problems are open-ended, so the modeler must be specific in defining what it is they would like to find out.

Define Variables
Making assumptions helps reveal the variables that will be needed. Limit the number of variables; start with only the most important.

Get a Solution
Eventually, a relationship between variables must be established to find a solution.

Analyze the Solution
When considering the results and insights gained from the model, ask if the answer makes sense.
Iterate
Refine the model by repeating the process, adjusting as needed to improve the solution.

Communicate
A clear report on the model and its implementation makes the model understandable to others.
Want more information? Check out this one-page summary of the math modeling process. Dig in even further by reading these free math modeling handbooks for newbies!
Video Series
What is Math Modeling?
Check out this quick how-to video series featuring students working through the components of the modeling process!
Video Series
Essentials of Math Modeling
For a deep dive into the modeling process, watch Essentials of Math Modeling, a seven-part workshop series focused on students, and featuring technical computing with MATLAB. The first hour of each is instructional and most valuable. Second part is interactive/working through parts of problems.




